|
:: 게시판
:: 이전 게시판
|
이전 질문 게시판은 새 글 쓰기를 막았습니다. [질문 게시판]을 이용바랍니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
10/05/25 17:16
간단하게 말씀드리면...
수조에서 유출구의 유속을 생각하면 되는건데요(유출구의 단면적이 같다고 가정하셨으니까) 이 때 유속은 유출구부터 수위까지의 높이차로 계산됩니다. V=c√(2gH) 로 계산하고... c = 감소계수 g = 중력가속도 H = 유출구 중심에서부터 수위까지의 높이 입니다...^^
10/05/25 17:25
첫번째에 차이없습니다. 이론적으로 베르누이의 공식을 보시면 압력, 위치에너지(높이)와 운동에너지(세기? 물의 속도)가 균형을 이뤄야 함을 알수있습니다. 노즐에서는 압력은 기압과 동일하고 물통안에 가스가 차있는게 아니고 보통 기압과 동일하다고 치면 같은 높이에서 나오는 물은 "노즐의 크기가 같을 경우" 같아야 정상입니다.
두번째는 말씀하신대로 물이 충분하게 있다는 가정하에 보면 세기는 같고 구멍이 여러개인쪽에서 두배는 빠르게 물이 소모될것같네요.
10/05/25 17:44
이재열님// 네... 유출구에서의 유속은 유출구의 형상이 같다는 조건에서는 오직 높이에 의해서만 결정됩니다.
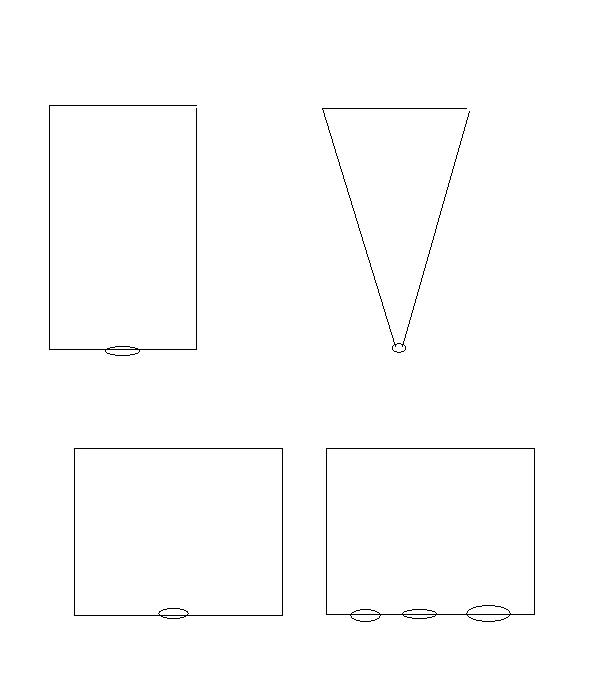
(c = 감소계수 이것이 유출구의 형상에 따라 달라지는 계수입니다) 어디선가 사진을 본 것이 기억나는데... 유출구의 높이를 달리했을 때는 나오는 물의 세기가 달랐는데... 유출구의 높이를 같이했을 때는 몇개를 뚫던지간에 물의 세기가 같은 사진이였죠.
10/05/25 18:14
세기라는 측면에서 본다면 다르게 생각할 수 있을 거 같은데요?
힘 = 질량 × 가속도 또는 힘 = 질량 × (속도)^2 / 2 이니까요...
즉 질량을 크게 해주는 방법(유출구의 단면적을 넓혀서 나오는 물의 양을 많이 하는 방법)이죠... 하지만 조건에 유출구의 단면적은 일정하다고 한다면... 물의 높이를 높게 해서 속도를 빠르게 하는 방법 뿐이네요;;;
10/05/25 18:57
탱크안에 압력을 가할수도 있죠. 수력발전용이라 하시면 탱크사이즈가 어마어마할 것같아서 좀 힘들지도 모르겠군요.
그리고 구멍을 어떻게 뚫으시느냐에 따라 조금씩 차이가 생깁니다. 참고하세요. http://www.jegasho.net/rotron%20pages/orifice%20flow%20calculation.htm
10/05/25 19:27
어떻게 수력 발전 시스템을 설계하실지는 모르겠지만, 보통 이런 경우에 속도를 빠르게 하는 것은 큰 의미가 없습니다. 어차피 에너지는 정해져 있는 것이고, 물을 작동유체로 하는 터빈이라면 노즐이라는 것이 쓸모가 없으니(비압축성이므로) 터빈 앞부분을 제작하는 데 그리 큰 고려를 할 필요는 없어 보입니다. 그냥 파이프 손실을 최소화하고 터빈의 효율을 가장 높일 수 있는 속도로 만드는게 가장 좋은 설계이겠죠.
|
||||||||||||