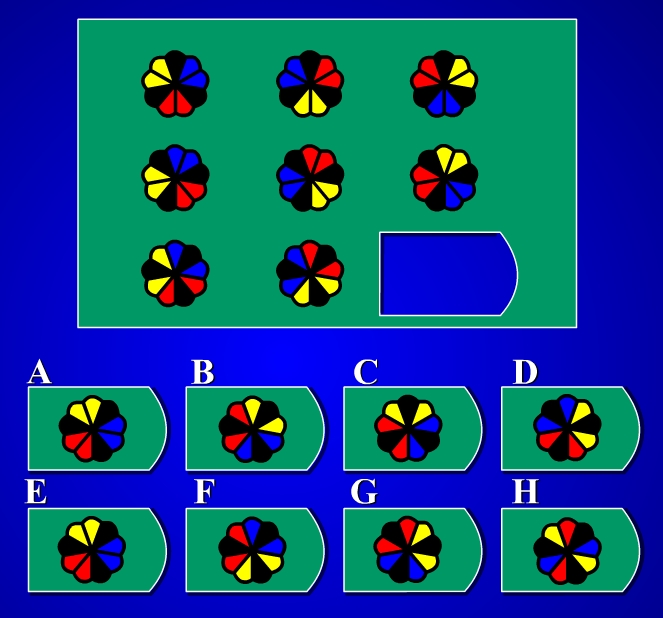
출처: http://www.iqtest.dk/main.swf

먼저 제가 올린 도형 퍼즐을 열심히 풀어주신 여러분께 감사를 표합니다.
도형 퍼즐을 처음 접하신 분들께 도움을 드리기 위해 일부 퍼즐 제작 과정(추론 퍼즐)과 팁을 공개합니다.
  
도형을 추론하는 문제의 난이도에 영향을 미치는 요소는 크게 3가지가 있습니다.
1. 규칙의 종류
2. 여러 규칙의 복합 적용 여부
3. 사용된 도형의 종류와 수

일반적으로 3가지 조건을 가지고 문제의 난이도를 조정하지요. 위에 나열된 조건들을 까다롭게 적용한다면 문제의 난이도는 아마 대단히 높아질 겁니다. 한 예로 제가 예전에 출제했던 도형 문제를 들 수 있겠지요.

https://pgr21.net/zboard4/zboard.php?id=humor&page=2&sn1=&divpage=17&sn=on&ss=on&sc=on&keyword=TimeLord&select_arrange=headnum&desc=asc&no=102248
(이 문제를 푸신 비비안님은 도형 퍼즐에 대단한 재능을 지니고 계신 듯..)

https://pgr21.net/zboard4/zboard.php?id=humor&page=1&sn1=&divpage=17&sn=on&ss=on&sc=on&keyword=TimeLord&select_arrange=headnum&desc=asc&no=102269

도형 퍼즐을 자세히 살펴본다면 두 가지 유형의 규칙이 보일 겁니다. 첫째는 언어 - 분석적 규칙이고 두 번째는 공간적 규칙이지요. 어떤 추상적인 도형이 무슨 의미를 담고 있는지 정확히 파악해야 하기 때문에 언어 - 분석적 규칙을 적용한 문제의 난이도가 좀더 높습니다. 위에 첨부한 2개의 도형퍼즐을 보시면 전자는 언어 - 분석적 규칙을 적용했고 후자는 공간적 규칙을 적용한 것을 쉽게 알 수 있을 겁니다.

어려운 문제의 경우 분석적 규칙, 공간적 규칙이 둘다 이용되는데 이런 퍼즐을 풀기 위해서는 먼저 도형의 변화를 자세히 살펴보는 것이 필수입니다. 일종의 어떤 대칭성을 찾는 것이지요. 그러면 그걸 바탕으로 정교한 규칙 생성 과정이 요구되는데 이때 시간이 많이 걸립니다. 실제로 제한시간을 두고 문제 푸는 것을 요구하면 많은 사람들이 당황을 하지요.

사실 쉬운 문제들에 도형 퍼즐을 푸는 아이디어는 모두 들어있습니다. 그걸 바탕으로 응용하는 것이 문제이지요. 일반적으로 말하자면 쉬운 규칙 2개를 결합시켰다고 해서 그 문제의 난이도가 여전히 쉬우리라고 기대할 수는 없습니다. 도형의 위치와 미묘한 변화에 따라 문제의 난이도가 좌우되기 때문이죠. 그런 규칙들의 조화를 잘 알아차리는 것이 도형 퍼즐의 묘미이기도 하지요.

마지막으로 한마디 덧붙이자면 이런 퍼즐은 재미로 푸는 것이라는 점을 꼭 말씀드리고 싶습니다. 퍼즐이 잘 안 풀린다고 스트레스 받을 것도 없고 그런 것이 퍼즐의 취지에 바람직하지도 않습니다. 그저 즐기는 목적으로 풀 때 아마 진정으로 퍼즐의 가치를 깨닫는 것이 아닐까 생각을 해 봅니다.