|
:: 게시판
:: 이전 게시판
|
- PGR21 관련된 질문 및 건의는 [건의 게시판]을 이용바랍니다.
- (2013년 3월 이전) 오래된 질문글은 [이전 질문 게시판]에 있습니다. 통합 규정을 준수해 주십시오. (2015.12.25.)
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
24/07/12 07:49
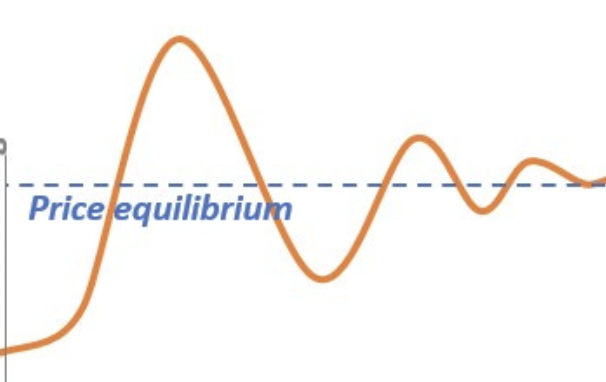
(수정됨) 진동하는 함수는 다항식으로는 표현이 안되고
y=-asin(x)/x^b 정도로 표현이 될 것 같네요. https://www.wolframalpha.com/input?i2d=true&i=y%3D-Divide%5BSin%5Bx%5D%2Cx%5D
24/07/12 08:05
제가 이해를 잘한건지 모르겠지만(수학을 그리 잘하는 것도 아니구요),
y축이 로그스케일이라고 하셨으니 y = log(y') = -asin(x)/x^b에서 y' = e^(-asin(x)/x^b)정도 되지 않을까요? 저도 확신은 없네요 크크
24/07/12 08:45
시작 부분을 보면 일반적인 sin함수는 아닌 것 같긴 합니다만, 그 부분 무시하면 그냥 적당히
y = -cos(x) * exp(-x/a) + b 정도로 기술하시면 유사한 그래프가 나올겁니다.
24/07/12 08:51
y=-cos(pi x) / 1.5^x
https://www.wolframalpha.com/input?i2d=true&i=y%3D-Divide%5Bcos%5C%2840%29pix%5C%2841%29%2CPower%5B1.5%2Cx%5D%5D 정도 해보세요. pi 를 곱하는게 물결 주기는 2로 맞춰주고요. 1.5 는 한 물결 이동할 떄마다 진폭이 1.5^2배 줄어든다는 의미입니다. 전체식에 첫 진폭 값 (가격 변동값; a) 을 곱하고, 평균 가격 (b) 을 더해주면 원하시는 그래프 나올 듯요 y=-a cos(pi x) / 1.5^x + b
24/07/12 08:53
y = - sin(x) / x
도 비슷하게 나옵니다. https://www.wolframalpha.com/input?i=-sin%28x%29%2Fx 다항함수로 전개할수도 있는데 이경우 x가 커질때 항상 오차가 커지게 됩니다. sin 테일러급수 로 검색해보세요
24/07/12 13:45
y = -cos(x) * (1 - x/2pi)
위의 수식을 0~2pi 까지 그리면 딱 저런 모양이 나올 것 같긴 하네요. 게임만들때 많이 써먹었던 스타일의 감쇄함수인데..
24/07/12 16:50
-cos x/x 정도 생각하고 있었습니다.
좋은 식은 다른 분들 만이 얘기해주신 거 같고 Gpt4o는 아래와 같이 얘기해주네요 ——————————— 이 이미지에서 나타난 노란색 선은 진동하는 감쇠 진동을 나타내는 것으로 보입니다. 이를 표현할 수 있는 일반적인 수식은 감쇠 진동을 설명하는 미분 방정식으로, 다음과 같이 나타낼 수 있습니다: [ y(t) = A e^{-gamma t} cos(omega t + phi) ] 여기서: - ( A )는 진폭 (amplitude) - ( gamma )는 감쇠 계수 (damping coefficient) - ( omega )는 각주파수 (angular frequency) - ( phi )는 위상 (phase) - ( t )는 시간 (time) 이 식은 시간 ( t )에 따른 진동하는 시스템의 위치 ( y(t) )를 나타냅니다. 위의 그래프에 정확하게 맞추기 위해서는 각 매개변수를 적절하게 조정해야 합니다.
|
||||||||||||